200以上 数学 円の面積の求め方 351405

数学の伝道師 秋山仁さん 算数を勉強しないと損 子どもを算数好きに育てるには 親子で挑む 算数つまずき攻略法 朝日新聞edua

 この式は、 a a の長さの直線を幅 b b まで足し合わせたものと見ることができます。 A = ∫ b 0 adx = a ⋅(b −0) = ab A = ∫ 0 b a d x = a ⋅ ( b − 0) = a b 同じ発想で、円の面積について考えてみましょう。 円を円周を足し合わせたものとして見るわけです。 半径 r r の円の円周は、 ℓ(r) = 2r⋅ π ℓ ( r) = 2 r ⋅ π となります。 そもそも円周率 π π は、円周 ℓ(r楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは（ @t_kun_kamakiri ）。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り

数学 円の面積の求め方

数学 円の面積の求め方-おうぎ形の面積と弧の長さを求める電卓 参考 円周率（314）のかけ算（314×1から314×128まで） 半径と円の面積の一覧表 円すい（円錐）の体積の求め方と問題 図形の面積（体積）や周りの長さを文字式にする問題まとめ27/9/19 一体なぜ成り立つのでしょうか？ それを知るには、面積や体積を決める ある要素 に注目する必要があるのです。 今回は例として 「長方形」「円」「三角錐」 を挙げてみました。 確かに、面積は「たて×横」ですし、体積は「たて×横×高さ」になってますね。 ※円周率 π π や三角錐の体積で出てくる 1 3 1 3 などの数は定数 (決まった数)なので、変化する

1

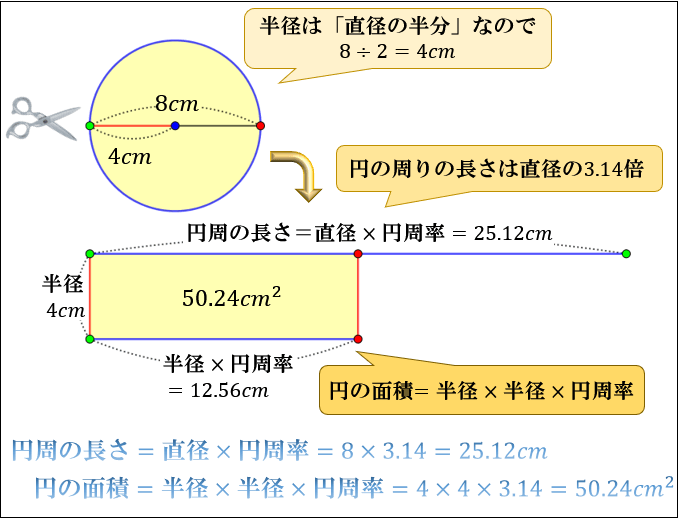
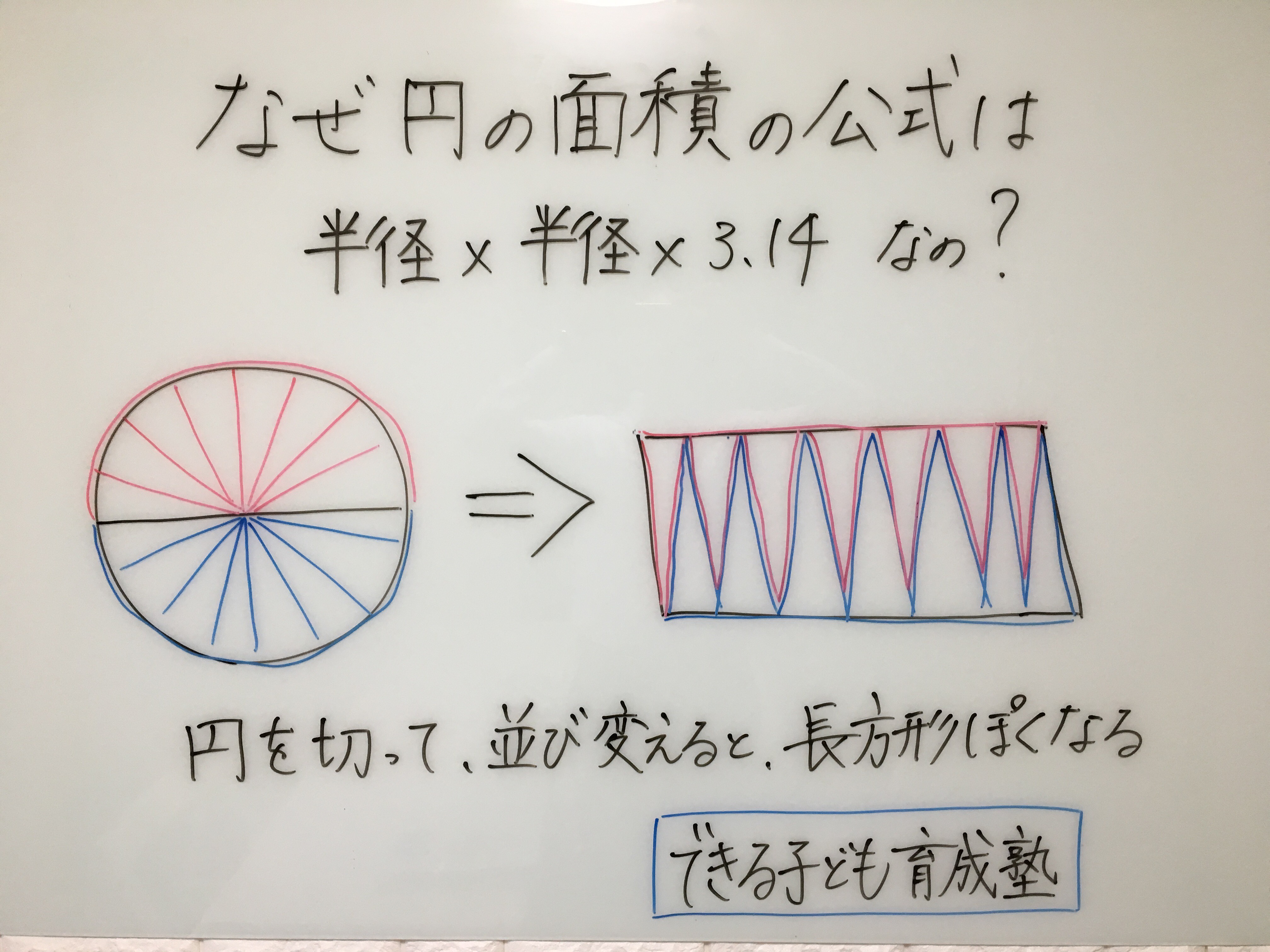
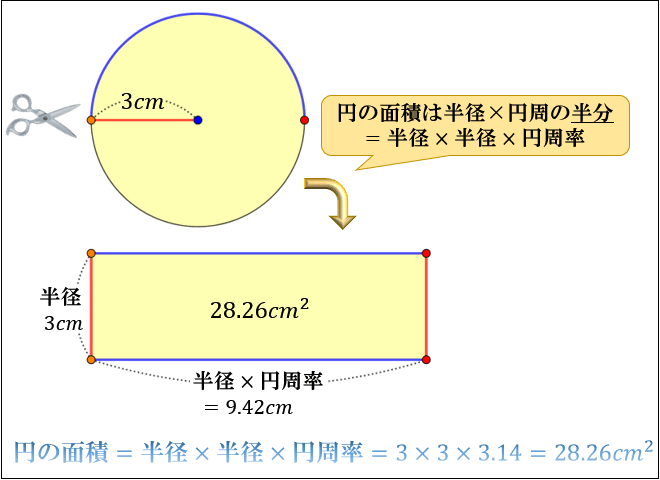
 円すいの表面積の求め方の手順とポイントがよくわかりません。 進研ゼミからの回答 次の3つが大きなポイントです。 ・底面（円）と側面（おうぎ形）に分けて求める ・円の円周とおうぎ形の弧の長さが同じ ・おうぎ形円の中心、半径を求める練習問題！ まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる！ こちらの関連記事はいかがでしょうか？14/3/15 円の面積 = 半径 × 半径 × 円周率 ってならったはずだ。 たとえば、半径3cmの円がいたとすると、コイツの面積は、 3×3×314 = 26 cm2 になるんだったね？ ？ 円の面積 = 半径 × 半径 × 円周率 っていう公式さえ覚えていればどうにかなるけど、これを忘れるとイタい。 あせる。

円の面積を求める公式は、S = πr^2 で表されます。このページでは、円の面積の求め方を、計算問題と共に説明しています。また、公式の導き方のイメージも説明しています。19/2/21 楕円の面積の公式は、主に \(2\) 通りの方法で導くことができます。 証明①図形の拡大・縮小 \(1\) つ目は、図形の拡大・縮小の考え方を利用します。 ただし、この証明では円の面積の公式が成り立つことが前提です。25/3/19 中学数学扇形の中心角の求め方3パターンピザでわかる 中心角は、円と扇の円周比を使って $2\pi r 2\pi l = x 360$

数学 円の面積の求め方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	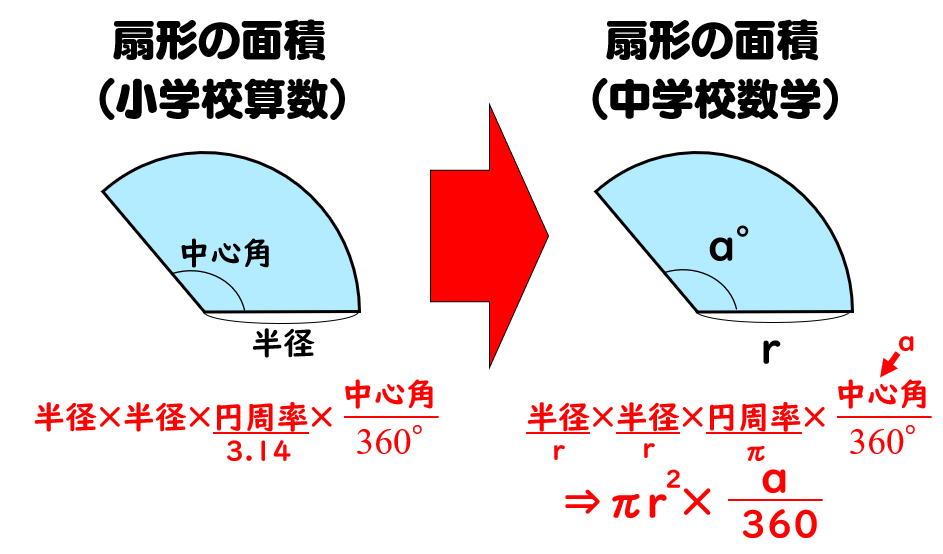円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	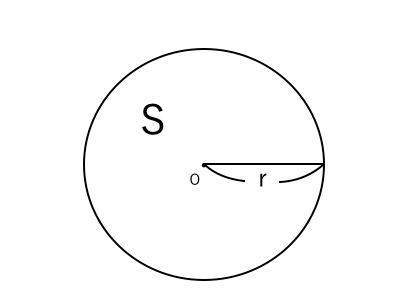円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	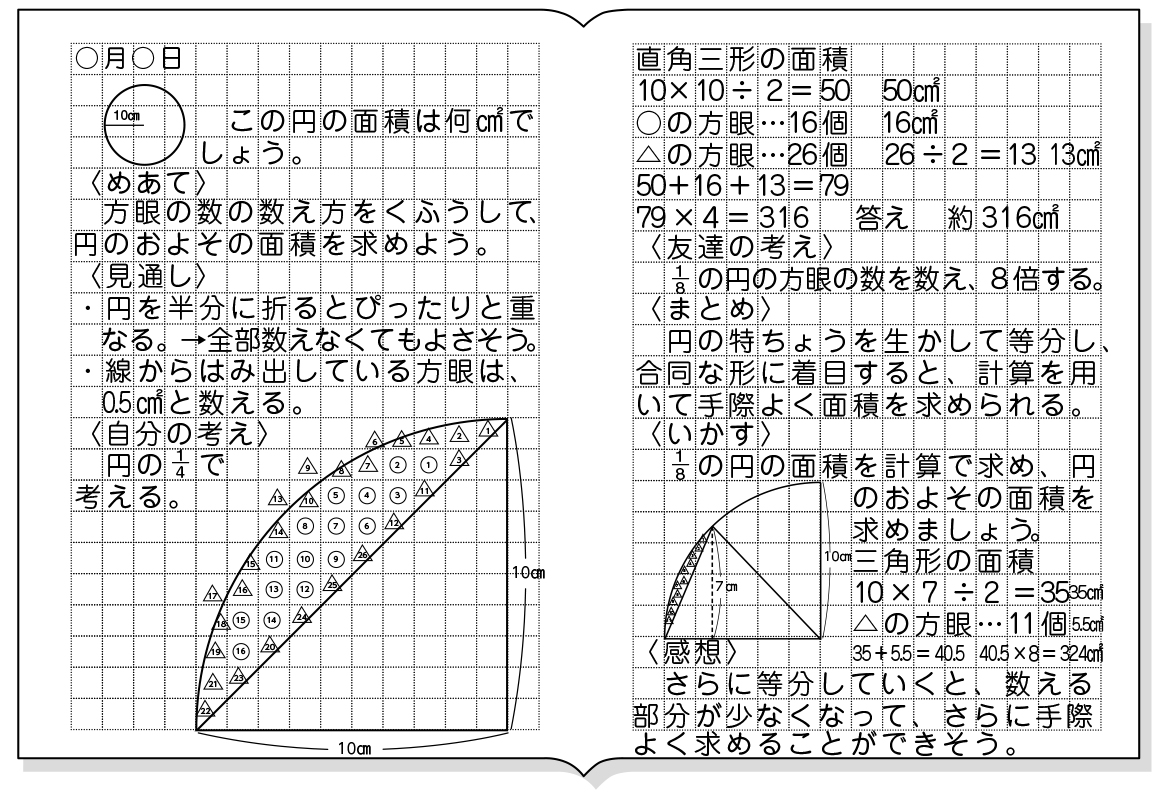円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に
円の面積 円周の求め方 苦手な数学を簡単に	円の面積 円周の求め方 苦手な数学を簡単に

21/2/18 円の面積の求め方公式 円の面積を求めるときには次の公式を使います。 円の面積＝半径×半径×円周率 （円周率は小学校ではふつう314を、中学の数学ではΠ（パイ）を使います。） スポンサードリンク 円の面積・円周の長さを求める問題6/3/21 1辺の長さは内接円の半径 r r である。 面積で考える方法も，接線の長さで考える方法も，どちらも同じくらい楽しいです。 高校数学の美しい物語の管理人。 「わかりやすいこと」と「ごまかさないこと」の両立を意識している。 著書に『高校数学の