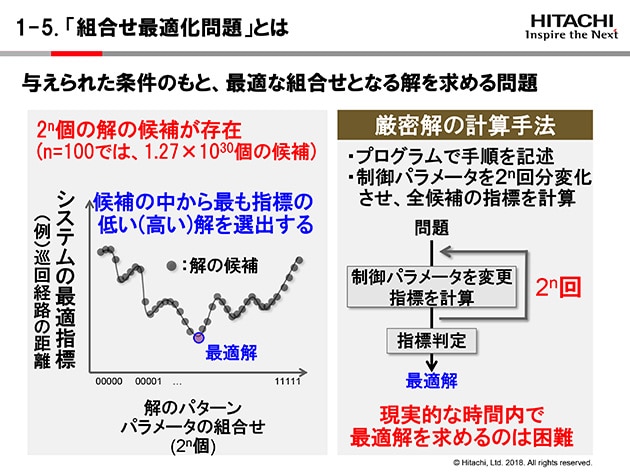
組合せ 場合の数において、最重要の「組合せ」 練習問題を通じて、理解を深めましょう。 例題1 \(6\) 人を、\(a,b\) の \(2\) つの部屋に分ける。次の問いに答えなさい。 (1)\(a\) に \(4\) 人、\(b\) に \(2\) 人となる分け方は全部で何通りありますか。精度保証付き近似解法 最大化問題 OPT 最適値 Obj アルゴリズムで得られる目的関数値 OPT/Obj このアルゴリズムの どんな問題例に対しても,OPT/Obj ≤ αを満たすとき,このアルゴ リズムを という. 最小化問題に対しては,Obj/OPT≤ αを満たすαで評価する. 5 章(組合せ最適化問題) 近似解法12 組合せ 3 証明 n1 ns 個のものの順列の個数は,(それら一つ一つが異なるものとみなした 場合)(n1 ns)!
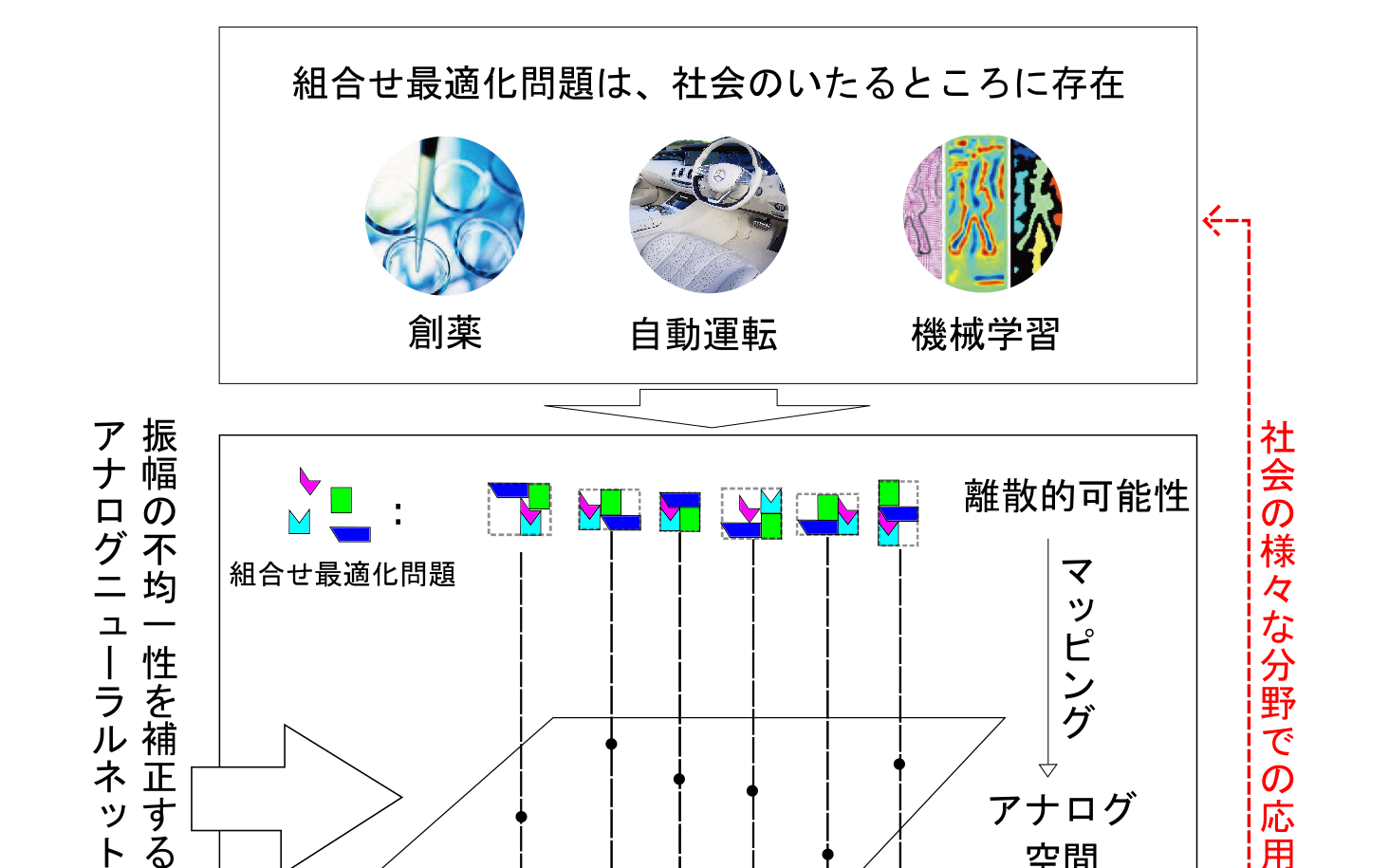
組合せ最適化問題を効率的に解くための新しいアナログニューラルネットワーク 東京大学生産技術研究所
組合せ問題 定式化 方法
組合せ問題 定式化 方法- この連載では、 fpga の応用事例として、「組合せ問題」を高速に解く試みについて触れていきます。 fpga のアプリケーションとしては、画像処理や深層学習 (いわゆるai) などが有名ですが、組合せ問題を fpga で高速に解こうという試みは fpga 研究の比較的早い時期 (90年代末) に起こり、^ 「外国人乗員問題」 日本航空機長組合 ^ 日航、旧jas系と統合へ 6労組に 共同通信10年4月22日 ^ 『jal再建 組合とビジネスプランが大問題』 日経bpビズカレッジ10年1月29日 ^ a b 池田信夫 エコノmix異論正論『jal年金問題は日本経済の縮図』 ニューズウィーク




Spi 場合の数 問題1 1 組み合わせ Study Pro Spi
順列・組合せの問題に挑戦! 順列・組合せの問題は、確率論、計算数学、オートマトンの理論および数理経済学において きわめて重要である。しかし、現行の教育課程においては、深く考えさせる問題が少なく、十 分な訓練ができる状況にはない。– 組合せ最適化問題とその応 – 計算困難な組合せ最適化問題に対するアプローチ – 規模な組合せ最適化問題に対する発的解法 講演途中でいくつかスライドをばすかも知れませんが ,本講演のスライドはウェブ上で 公開する予定なのでご安下さい .よく「順列」と「組合せ」を間違って用いられている場合がありますので,慎重に扱って下さい(心の中で,順列 を扱っているのだ,組合 を扱っているのだ,という自覚をもちましょう)。 では,組み合わせの問題を考えていくことにします。 次の例を見て下さい。 ここでも,前章と同じ,メンバーに登場してもらうことにしましょう。 例1 5人から3人を選ぶ
典型的な重複組合せを用いる問題として,整数解の個数を求めるタイプの問題があります. 例題 xyz = 8 x y z = 8 を満たす非負整数 (0 0 以上の整数)の組 (x,y,z) (x, y, z) の総数を求め (2)組み合わせ問題において「少なくとも1人(1つ)〜」を求めるときは、 組み合わせの総数 から 1人(1つ)もない 場合 を引く事でもとめる場合が多いです。 組み合わせの総数は(1)で求めたので、今回は男子だけを3人選ぶときを考えます。田中:組合せ最適化問題とスケジューリング 1 回路となる保証はない.したがって01ベクトルのうち, 巡回路に対応するものだけを集めた集合がfとなる. 組合せ最適化では通常,有限のfを考えるので,原理 的にはすべての要素を列挙すれば最適解が求まることに
組合せの最も基本的な事柄と,よくある組合せの問題を解説します. 組合せとは いくつかのものからいくつかのものを取り出して 並べる ことを 順列 と呼んでいました.ここでは,取り出したときの順序を考えない場合の数を考えてみましょう.そのような問題は 組合せ の問題と呼ばれてならべ方・組み合わせの問題の違い 小学校で習う「場合の数」では主に 『ならべ方(順列)』 の問題と 『組み合わせ』 の問題があります。 これらは似たような問題ですが、解き方が異なるのでまずは見分けがつかないと解くことができません。組分け問題の解き方 組分け問題は以下の2つのステップを踏むことで必ず解くことが出来ます! つまり先程イラストで解説した、振り分け先の区別の有無に関わらず、 まずstep1では 全ての部屋が区別できるとして各部屋に人を振り分けていきます




問題の組合せは無限大 アウトレット品 面体の数学パズル 知育玩具 6歳 ボーネルンド社 数字ロジックパズル 入園 おうち時間 お誕生日 アイコゾク 子供 入学



3
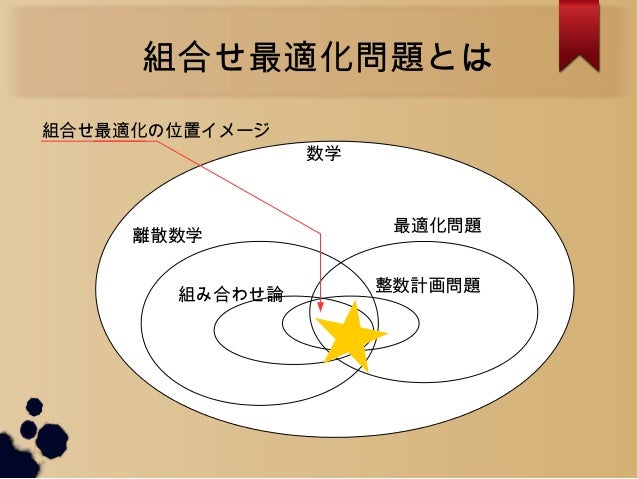
組合せ最適化 (くみあわせさいてきか、 英 combinatorial optimization 、 組み合わせ最適化 、または 組み合せ最適化 とも表記される)は、 応用数学 や 情報工学 での 組合せ論 の 最適化問題 である。組合せ数学(くみあわせすうがく、英語 combinatorics )あるいは組合せ論(くみあわせろん)とは、特定の条件を満たす(普通は有限の)対象からなる集まりを研究する数学の分野。 離散数学の中核の一つとされる。特に問題とされることとして、集合に入っている対象を数えたり(数え上げ的それくらい、「順列」と「組合せ」は大事です。 「場合の数」では、基本的な考え方が最重要となってくるので、本記事で、「順列」や「組合せ」の基礎をマスターさせましょう。 例題を通して、説明していくので、ぜひ例題にもチャレンジしてみてください。 この記事の内容 場合の数の「順列」と「組合せ」の公式 「順列」と「組合せ」の違い 「順列」と




今日から使える 組合せ最適化 離散問題ガイドブック Ks理工学専門書 穴井 宏和 斉藤 努 本 通販 Amazon
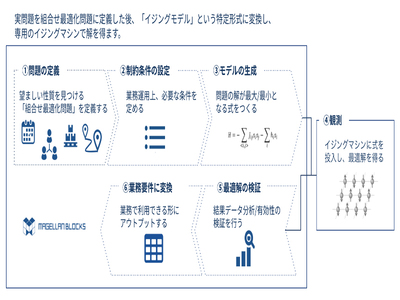



グルーヴノーツ 組み合わせ最適化問題を解くクラウドサービスを強化 イジングマシンを拡充 It Leaders
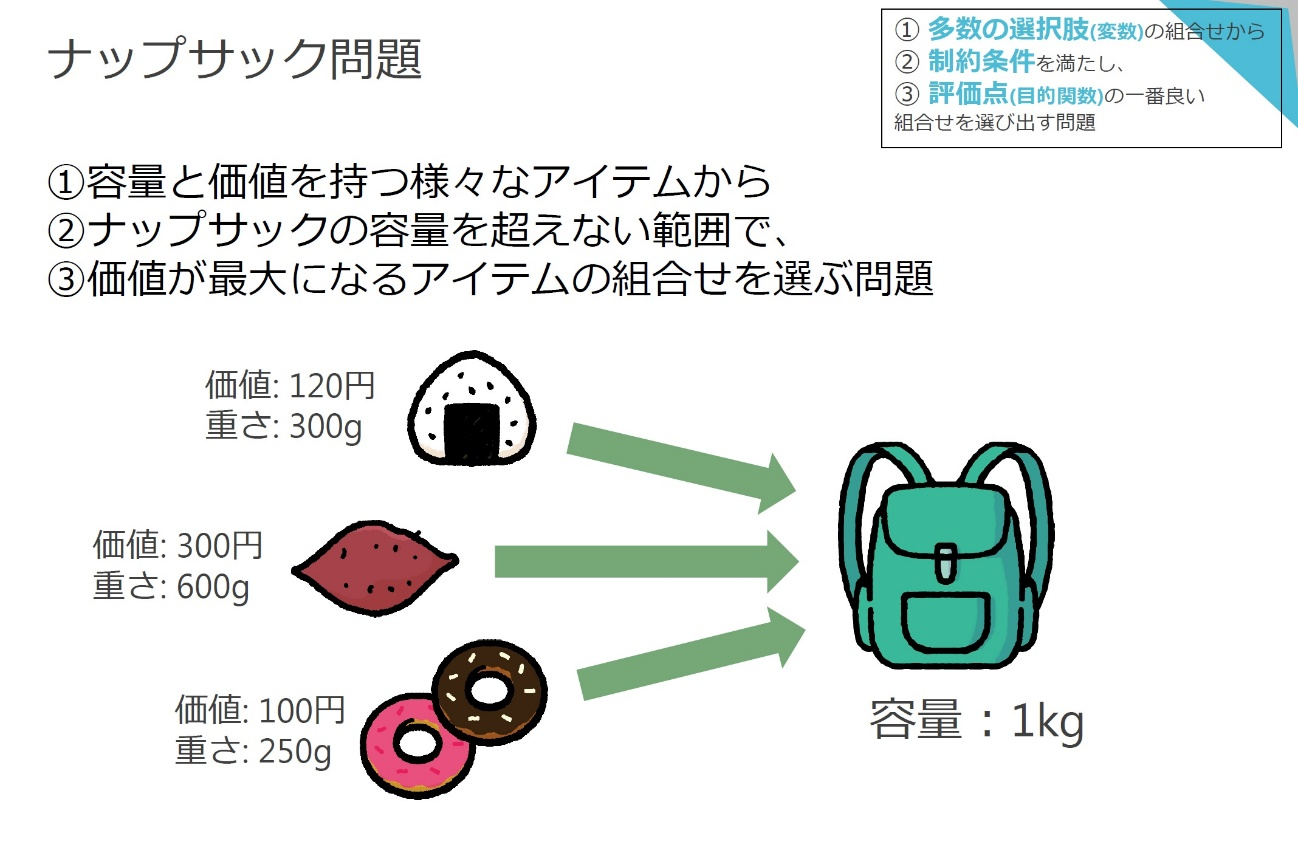
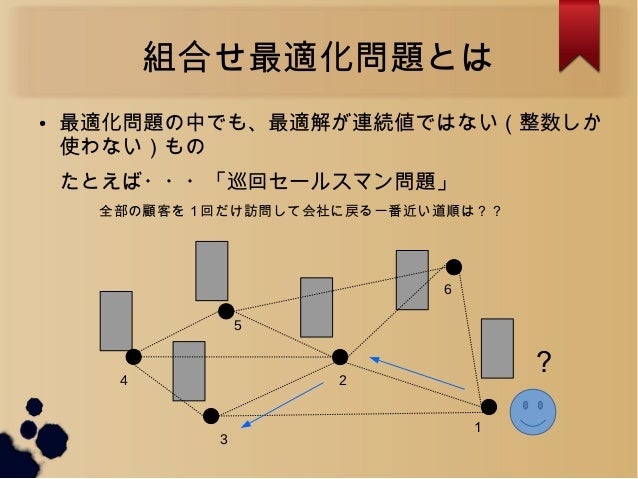
組合せ最適化問題 まず, 最適化問題とは「条件を満たす解の中で一番よいものを求める問題」 を指します.さらに, 組合せ(離散)最適化とは「解が順序や割当のように 組合せ的な構造を持つ最適化問題」 のことを言います. 練習問題 順列と組合せの問題を混ぜました。順列と組合せの違い 順列 :「選んで並べる」「abとba を区別してそれぞれ数える」 組合せ :「選ぶだけで並べない」「abとbaは区別せず同じもの」 に注意しながら,考えてみてください。重複組合せの例題です。 青,赤,黒それぞれ何回でも使えます (重複を許す) 。 順番は区別しません(順列ではなく 組合せ )。例えば「青青赤青」と「青青青赤」は区別せず同じパターンとみなしま




組合せ最適化問題 をアニーリング方式で解決する デジタルアニーラ とは デジタルアニーラ 富士通



進化する最適化技術 Vol 2 最適化問題を解決に導くnssolの技術と実績 量子アニーリングは万能ではない To The Future 日鉄ソリューションズ
である.そのうちのある順列˙ を考える.任意のi 2 s につい て,第i 種のものはni 回,˙ に出現する.それらni 個のものの順番を入れ替えたある 順列を˙′ とする.同種のものは初めに、その問題が順列なのか、組合せなのかを見分けます。 そのために、まず「順列」と「組合せ」とは何なのか考えてみましょう。 わかりmathでは、順列の問題を「 席の問題 」、 組合せの問題を「 組の問題 」と整理しています。順列・組合せ総合問題 練習問題19 5人の旅客が3件の旅館に泊まる泊まり方は何通りあるか。 ただし1人も宿泊しない旅館があってもよいとする。 上の問題において,人を仮に固定し,どの旅館に宿泊するか,ということを考えればよいのです。 発想の



組合せ最適化 一般人向けの解説




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学
組合せ列挙問題とは,要素集合から与えられた制約 を充足する要素の組合せ(解) をすべて求める問題で ZDDs and Enumeration Problems StateofTheArt Techniques and Programming Tool Takahisa Toda, 電気通信大学大学院情報理工学研究 科, Graduate School of Informatics and Engineer(2) 組合せ最適化問題への具体化(ステップ2) 抽出した課題から組合せ最適化問題として解く ことができる問題を抽出する。 (3) 定式化(ステップ3) 解決すべき問題に対して,一般によく知られて いる数十パターンの定式化済みの組合せ最適化問例 2桁の整数のうち, 87 , 51 のように十の位の数が一の位の数よりも大きなものの総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを選べば(組合せ)並べ方は決まる(大きい方を前にする)から 10C2=45 個 (別解) 十の位が1ならば一の位は0だけだから1通り,十の位が2ならば一の位は0,1の2通り,・・・,十の位が9ならば一の位は0,1,・・・,8の9通り.ゆえに



1




組合せ論パーフェクト マスター 日本評論社
例 2桁の整数のうち, 87 , 51 のように十の位の数が一の位の数よりも大きなものの総数 (解答) 10個の数字 0,1,2,3,4,5,6,7,8,9 から異なる2つを選べば(組合せ)並べ方は決まる(大きい方を前にする)から 10 C 2 =45 個 (別解) 十の位が1ならば一の位は0だけだから1通り,十の位が2ならば一の位は0,1の2通り,・・・,十の位が9ならば一の位は0,1,・・・,8の9通り.ゆえ順列と組合せの応用問題5選 それでは、ここからは順列と組合せの応用問題をごちゃまぜに $5$ 問解いていきたいと思います。 具体的には 委員の選出;このセクションでは、組合せ最適化問題を紹介し、近似最適化アルゴリズムの説明、Quantum Approximate Optimization Algorithm (QAOA)の動作説明、及びシミュレーターもしくは5量子ビットチップで動作する実装例の紹介をします。




原点の ベンチャースピリット で金融市場進出へ 東芝が開発した 最先端 の計算技術 開発の苦労とその勝算 偶然 が生み出した最先端技術 Itmedia ビジネスオンライン




重複組合せ 組合せ 重複順列に関する問題 2018年度前期日程高知工科大学の入試問題 身勝手な主張
「10人から2人の委員を選ぶだけ」 なので、「組合せ」の問題だということはわかるね。 これがもしも、 「10人から2人の委員を選んで、委員長・副委員長を決める」 という問題だったら、計算は簡単だったんだ。 順列 を使って 10 P 2 で求められる よね。組合せ を利用する頻出問題の5パターン目を解説していこう。 今回は、 組み分けの問題 だよ。 例えば、「9人の生徒を3人ずつ3グループに分けるときの総数」のような問題だね。組合せ最適化問題に対する 効率的な厳密解法のための問題の 記述法に関する研究 乾 伸雄 博士(情報学) 総合研究大学院大学




高校数学a 場合の数 組合せ頻出 男女を選ぶ問題 高校生 数学のノート Clear




組合せ最適化問題を効率的に解くための新しいアナログニューラルネットワーク 東京大学生産技術研究所
10人のメンバーを 4人、4人、2人 のチームに分ける組み合わせが何通りあるか、といった問題です。 一般的に書くと、次の式で求められます。 異なる \(n\) 個のものを、\(r_1\) 個、\(r_2\) 個、\(\cdots\)、\(r_i\) 個に分ける組み合わせ方は次の式で求められます。




Spi 場合の数 問題1 1 組み合わせ Study Pro Spi




難しくても使いこなす組合せ最適化 1 ー問題例と解き方ー Nttデータ数理システム




重複組合せ3 不等号の問題 Nhrの公式は不要 X Y Z 12 X 0 Y 0 Z 0 Youtube



Spi M54e217p7lcis9d Com Jyunretu Kumiawase Q1




組分け問題全パターン おいしい数学




組合せ最適化問題と解法アルゴリズム




数的処理 超 基礎講座 場合の数 組合せ 高卒程度公務員試験対策 数的推理 問題演習 重複組合せ Youtube



48s96ub7b0z5f Net Saitankeiro



組合せ最適化 一般人向けの解説




組合せの練習問題 高校数学の無料オンライン学習サイトko Su



書評 今日から使える 組合せ最適化 Tim Labs




今日から使える 組合せ最適化 離散問題ガイドブック Ks理工学専門書 穴井 宏和 斉藤 努 本 通販 Amazon




組合せ最適化問題 をアニーリング方式で解決する デジタルアニーラ とは デジタルアニーラ 富士通




順列pと組み合わせcの違いと 簡単 な見分け方



Fpga を用いた 組合せ問題 の高速計算 1 Acri Blog




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



2




重複組み合わせの問題を解くたった1つの方法とは 公式hは使用注意



重複組合せの考え方 思考力を鍛える数学



確率問題全般 京極一樹の数学塾




数学ia 組合せに関する問題の考え方 人の選び方 大学入試数学の考え方と解法




高校数学a 組合せの活用1 点を結ぶ 例題編 映像授業のtry It トライイット




順列と組み合わせの公式とその違い 問題付き 理系ラボ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



Cmosチップでアニーリングマシンを作製 組合せ最適化問題を解く 2 4 Telescope Magazine




組み合わせの考え応用 最短経路選択問題をシミュレーターで理解しよう 数学入門




富士通研究所 組合せ最適化問題向けアーキテクチャを開発 Zdnet Japan



組合せ問題最適化ソリューション Brms 徹底活用ナビ



数学i Aチェック リピート 第7章 2順列 組合せ 6 重複組合せ Pukiwiki



写像12相をいちから勉強してatcoderの組合せ 数え上げ問題をクリアしたいと思ったけどまだまだ知らない事が多いと強烈に感じた Ctoの日記




Cmosチップでアニーリングマシンを作製 組合せ最適化問題を解く 1 4 Telescope Magazine



数学i Aチェック リピート 第7章 2順列 組合せ 10 最短経路 Pukiwiki




楽天ブックス 超高速グラフ列挙アルゴリズム フカシギの数え方 が拓く 組合せ問題への新アプローチ 湊 真一 本




計算困難問題に対するアルゴリズム理論 組合せ最適化 ランタ マイセ ーション 近似 ヒューリスティクス Amazon Com Books



1



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください



00ノードの組合せ最適化問題 解探索に成功 量子ニューラルネットワーク 1 2 ページ Ee Times Japan




Title 組合せ最適化問題における近接最適性原理の定量的評 価と




高校数学a 組合せの計算1 Ncr 例題編 映像授業のtry It トライイット




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭




Spi 確率 問題1 1 組み合わせ Study Pro Spi




組合せ最適化問題とは Annealing Cloud Web



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




最適化問題入門 錐最適化 整数最適化 ネットワークモデルの組合せによる 委託 達人出版会



場合の数 学び家 Com




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学



光で組み合わせ最適化問題を解く 量子ニューラルネットワーク とは 5分で分かる最新キーワード解説 1 4 ページ キーマンズネット
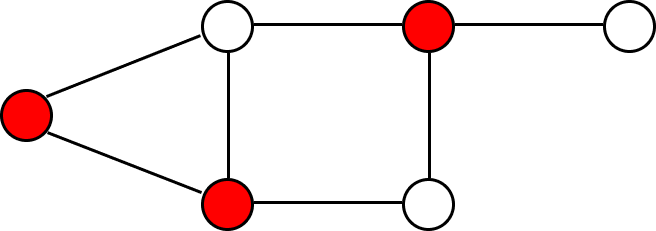



組合せ最適化問題 アーカイブ T Wave




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



希望考慮し全ペアいい組合せを見つける Thoth Children




順列と組合せの違いと例題 高校数学の美しい物語
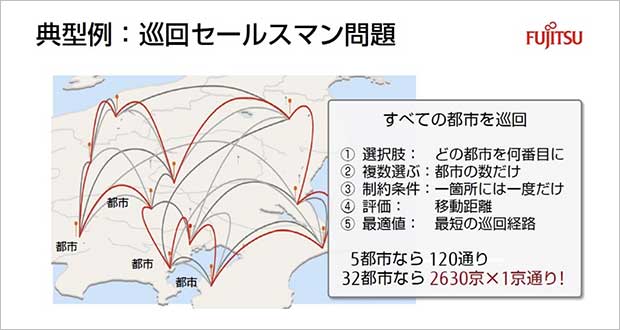



組合せ最適化問題 をアニーリング方式で解決する デジタルアニーラ とは デジタルアニーラ 富士通




今日から使える 組合せ最適化 離散問題ガイドブック 書籍情報 株式会社 講談社サイエンティフィク



同じものを含む順列の問題 京極一樹の数学塾
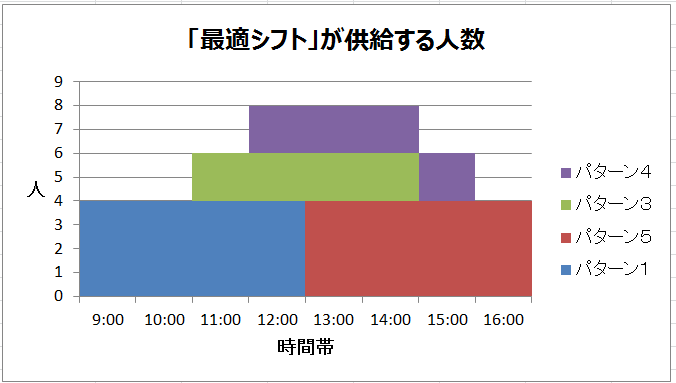



難しくても使いこなす組合せ最適化 1 ー問題例と解き方ー Nttデータ数理システム



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




数学a 場合の数 順列の問題か 組み合わせの問題かの見分け方 坪田塾 公式youtubeチャンネル Youtube




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




量子 と組合せ最適化に関する怪しい言説 とある研究者の小言 むしゃくしゃしてやった 今は反省している日記




高校数学a 組分け問題全パターン 受験の月




Msi株式会社 数理最適化ソルバー Xpress Lp Mip Localsolver 大規模組合せ最適化 の提供




トップ 100 並べ方 と 組み合わせ 方 問題



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典




社労士 択一式試験 組み合わせ問題 個数問題の解答テクニック 社労士試験 16 本試験問題の合格ライン予想



組合せ最適化 企業の人への解説
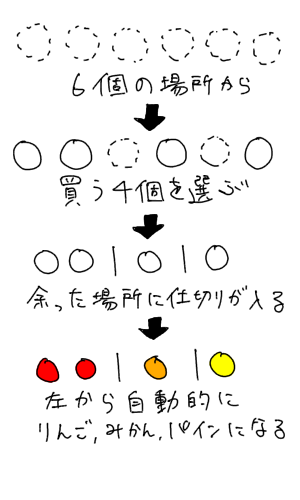



重複組み合わせは絵を描けば理解できる イラストで解説 理数白書




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




Ircn Utokyo 研究成果 組合せ最適化問題を効率的に解くための新しいアナログニューラルネットワーク 合原一幸主任研究者 雑誌名 Physical Review Letters T Co Kmpdadx6sk Ircn 東京大学 Utokyo 生産技術研究所 組合せ最適化




組み合わせ問題をjavaで 重複組合せ ジョイタスネット



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




組合せ最適化問題 をアニーリング方式で解決する デジタルアニーラ とは デジタルアニーラ 富士通




光を用いて組合せ最適化問題を解く新しい計算機コヒーレントイジングマシン Lasolv Ntt R D Website




知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



Cnnとgaを用いた 組合せ最適化問題




社内講演会レポ ト 組合せ最適化による問題解決の実践的なアプローチ Platinum Data Blog By Brainpad




高校数学a 重複組合せ Nhr 受験の月



Q Tbn And9gcsw Y9fcgx3auohhjlgzbsjd5szne8pubuaewn5ppyowdb2se08 Usqp Cau




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
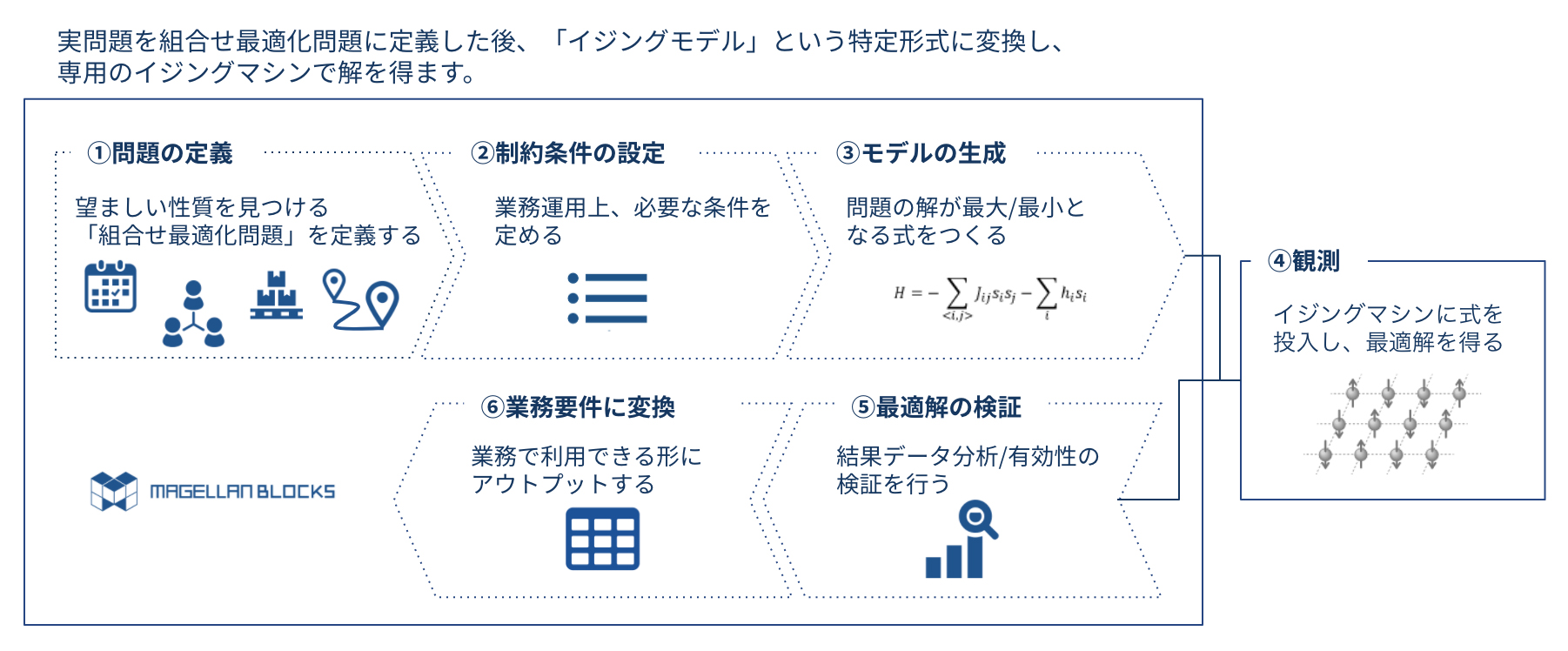



グルーヴノーツ 組み合わせ最適化問題を解くクラウドサービスを強化 イジングマシンを拡充 It Leaders




楽天ブックス 今日から使える 組合せ最適化 離散問題ガイドブック 穴井 宏和 本
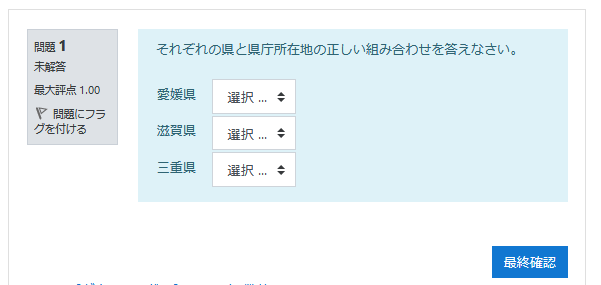



10 01 16 組み合わせ問題を追加する Waseda Moodle利用マニュアル




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学



Cnnとgaを用いた 組合せ最適化問題




北海道札幌厚別高等学校 数学応用 学校設定科目 順列 組合せの違いを理解する 竹之内 康秀教諭
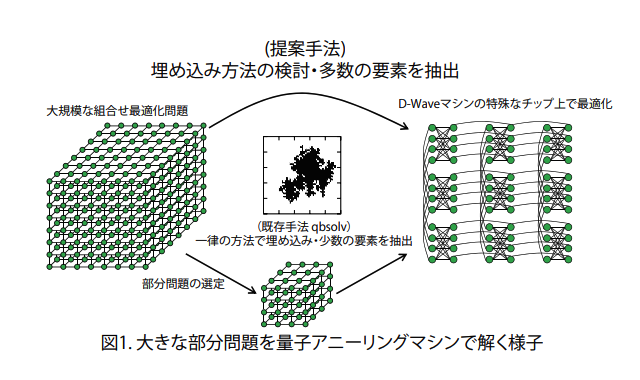



量子アニーリングマシンの効率的利用方法を開発 大規模な組合せ最適化問題を高精度に解く方法を考案 東北大学など Fabcross For エンジニア
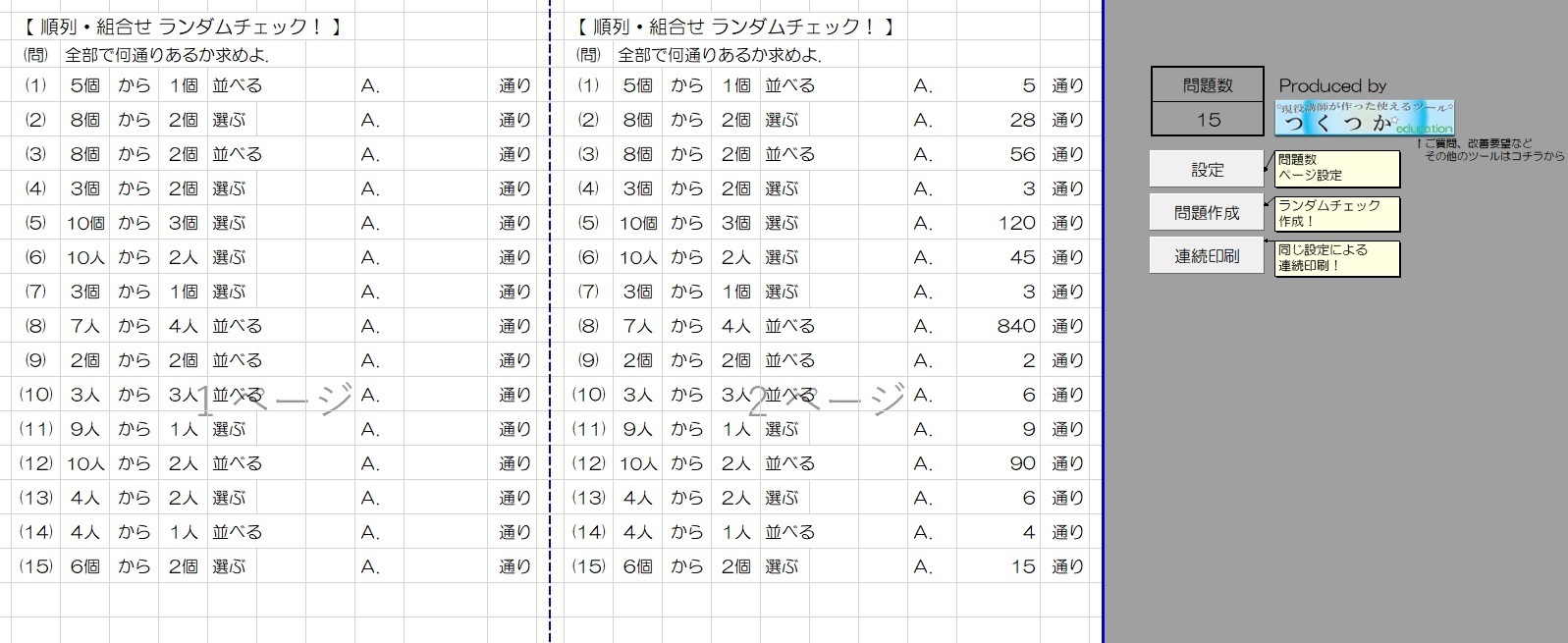



順列 組合せランダムチェック公開 現役講師が作った使えるサイト




Images Na Ssl Images Amazon Com Images I 41zy7u




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ
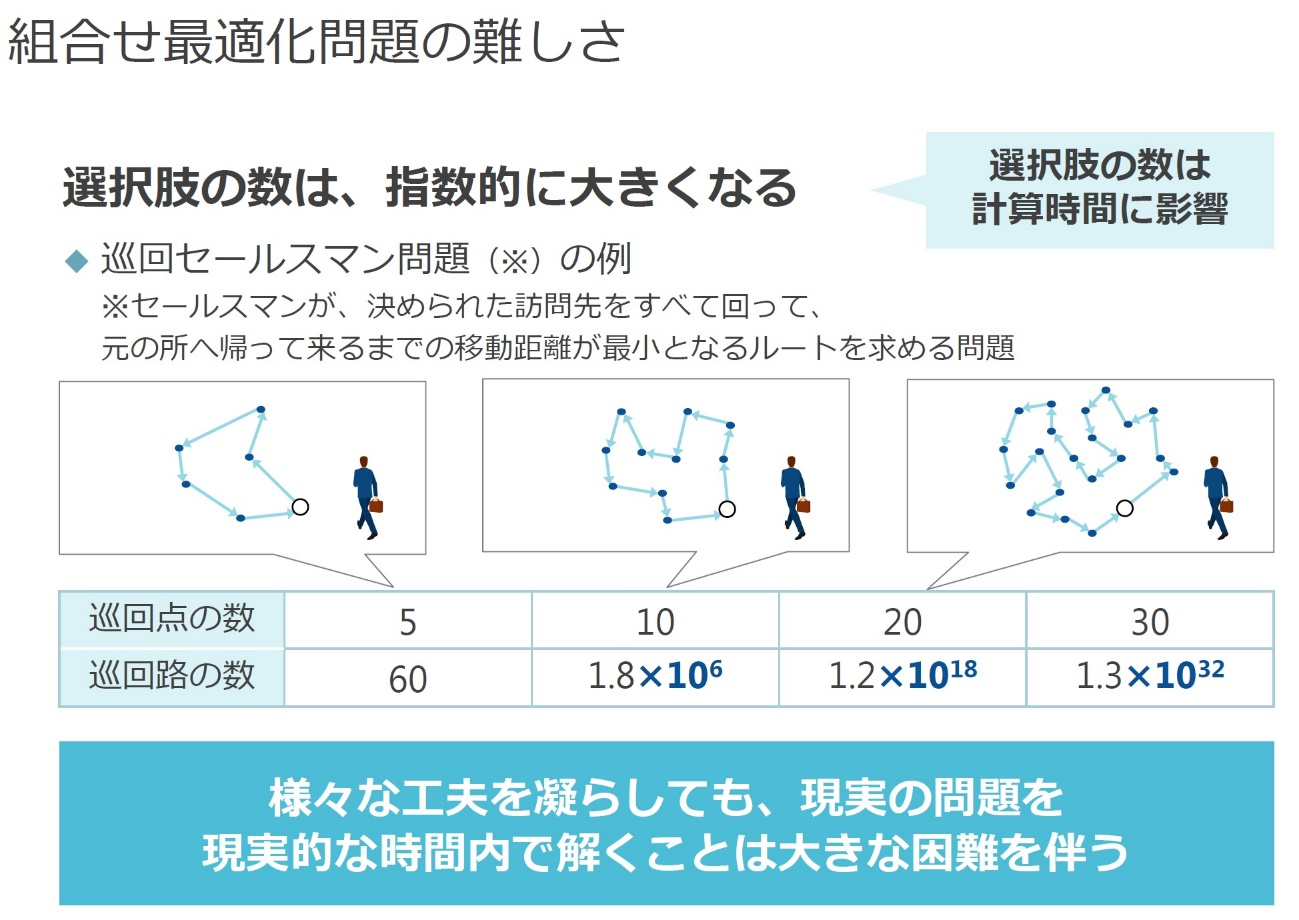



進化する最適化技術 Vol 2 最適化問題を解決に導くnssolの技術と実績 量子アニーリングは万能ではない To The Future 日鉄ソリューションズ



0 件のコメント:
コメントを投稿